A geosynchronous orbit is any orbit which has a period equal to the earth's rotational period. As we shall soon see, this requirement is not sufficient to ensure a fixed position relative to the earth. While all geostationary orbits must be geosynchronous, not all geosynchronous orbits are geostationary. One disadvantage of geostationary orbits is the great distance to the Earth, which reduces the achievable spatial resolution. Meteosat and other satellites in geostationary orbit There are a number of weather satellites evenly distributed in geostationary orbit all around the world to provide a global view. A geostationary orbit is an orbit which is fixed in respect to a position on the Earth. Therefore, the time period will always be 24 hours. From combining the centripetal force, gravitational force and basic velocity force equations, we can deduce that the radius required for a.
Geostationary/geosynchronous csatellites have revolutionized global communications (phone, internet) and TV broadcasting.
A geostationary satellite is an earth-orbiting satellite, placed at an altitude of approximately 35,800 kilometers (22,300 miles) directly over the equator, that revolves in the same direction the earth rotates (west to east). At this altitude, one orbit takes 24 hours, the same length of time as the earth requires to rotate once on its axis. The term geostationary comes from the fact that such a satellite appears nearly stationary in the sky as seen by a ground-based observer.

Other Iridium Phones:
A single geostationary satellite is on a line of sight with about 40 percent of the earth's surface. Three such satellites, each separated by 120 degrees of longitude, can provide coverage of the entire planet, with the exception of small circular regions centered at the north and south geographic poles. A geostationary satellite can be accessed using a directional antenna, usually a small dish, aimed at the spot in the sky where the satellite appears to hover. The principal advantage of this type of satellite is the fact that an earthbound directional antenna can be aimed and then left in position without further adjustment. Another advantage is the fact that because highly directional antennas can be used, interference from surface-based sources, and from other satellites, is minimized.
Derivation of geostationary altitude
In any circular orbit, the centripetal acceleration required to maintain the orbit is provided by the gravitational force on the satellite. To calculate the geostationary orbit altitude, one begins with this equivalence, and uses the fact that the orbital period is one sidereal day.
By Newton's second law of motion, we can replace the forces F with the mass m of the object multiplied by the acceleration felt by the object due to that force:

We note that the mass of the satellite m appears on both sides — geostationary orbit is independent of the mass of the satellite. So calculating the altitude simplifies into calculating the point where the magnitudes of the centripetal acceleration required for orbital motion and the gravitational acceleration provided by Earth's gravity are equal.
The centripetal acceleration's magnitude is:
where ? is the angular speed, and r is the orbital radius as measured from the Earth's center of mass.
The magnitude of the gravitational acceleration is:
where M is the mass of Earth, 5.9736 × 1024 kg, and G is the gravitational constant, 6.67428 ± 0.00067 × 10-11 m3 kg-1 s-2.
Equating the two accelerations gives:
The product GM is known with much greater accuracy than either factor; it is known as the geocentric gravitational constant µ = 398,600.4418 ± 0.0008 km3 s-2:
The angular speed ? is found by dividing the angle travelled in one revolution (360° = 2p rad) by the orbital period (the time it takes to make one full revolution: one sidereal day, or 86,164.09054 seconds).[3] This gives:
The resulting orbital radius is 42,164 kilometres (26,199 mi). Subtracting the Earth's equatorial radius, 6,378 kilometres (3,963 mi), gives the altitude of 35,786 kilometres (22,236 mi). Orbital speed (how fast the satellite is moving through space) is calculated by multiplying the angular speed by the orbital radius:
Orbite alocation
Satellites in geostationary orbit must all occupy a single ring above the equator. The requirement to space these satellites apart means that there are a limited number of orbital 'slots' available, thus only a limited number of satellites can be placed in geostationary orbit. This has led to conflict between different countries wishing access to the same orbital slots (countries at the same longitude but differing latitudes). These disputes are addressed through the International Telecommunication Union's allocation mechanism.[5] Countries located at the Earth's equator have also asserted their legal claim to control the use of space above their territory.[6] Since the Clarke Orbit is about 265,000 km (165,000 mi) long, countries and territories in less-populated parts of the world have been allocated slots already, even though they aren't used, yet. The problem presently lies over densely-populated areas such as the Americas and Europe/Africa, and above the middles of the three equatorial oceans.
Orbit Inclination
If a geosynchronous satellite's orbit is not exactly aligned with the equator, the orbit is known as an inclined orbit. It will appear (when viewed by someone on the ground) to oscillate daily around a fixed point in the sky. As the angle between the orbit and the equator decreases, the magnitude of this oscillation becomes smaller; when the orbit lies entirely over the equator, the satellite remains stationary relative to the Earth's surface – it is said to be geostationary.
Impact on signals
Satellites in geostationary orbits are far enough away from Earth that communication latency becomes very high — about a quarter of a second for a one-way trip from a ground based transmitter to a geostationary satellite and back, and close to half a second for round-trip end-to-end communication.
For example, for ground stations at latitudes of f=±45° on the same meridian as the satellite, the one-way delay can be computed by using the cosine rule, given the above derived geostationary orbital radius r, the Earth's radius R and the speed of light c, as
This presents problems for latency-sensitive applications such as voice communication or online gaming.
Application
There are approximately 300 operational geosynchronous satellites. Geostationary satellites appear to be fixed over one spot above the equator. Receiving and transmitting antennas on the earth do not need to track such a satellite. These antennas can be fixed in place and are much less expensive than tracking antennas. These satellites have revolutionized global communications, television broadcasting and weather forecasting, and have a number of important defense and intelligence applications.
One disadvantage of geostationary satellites is a result of their high altitude: radio signals take approximately 0.25 of a second to reach and return from the satellite, resulting in a small but significant signal delay. This delay increases the difficulty of telephone conversation and reduces the performance of common network protocols such as TCP/IP, but does not present a problem with non-interactive systems such as television broadcasts. There are a number of proprietary satellite data protocols that are designed to proxy TCP/IP connections over long-delay satellite links -- these are marketed as being a partial solution to the poor performance of native TCP over satellite links. TCP presumes that all loss is due to congestion, not errors, and probes link capacity with its 'slow-start' algorithm, which only sends packets once it is known that earlier packets have been received. Slow start is very slow over a path using a geostationary satellite.
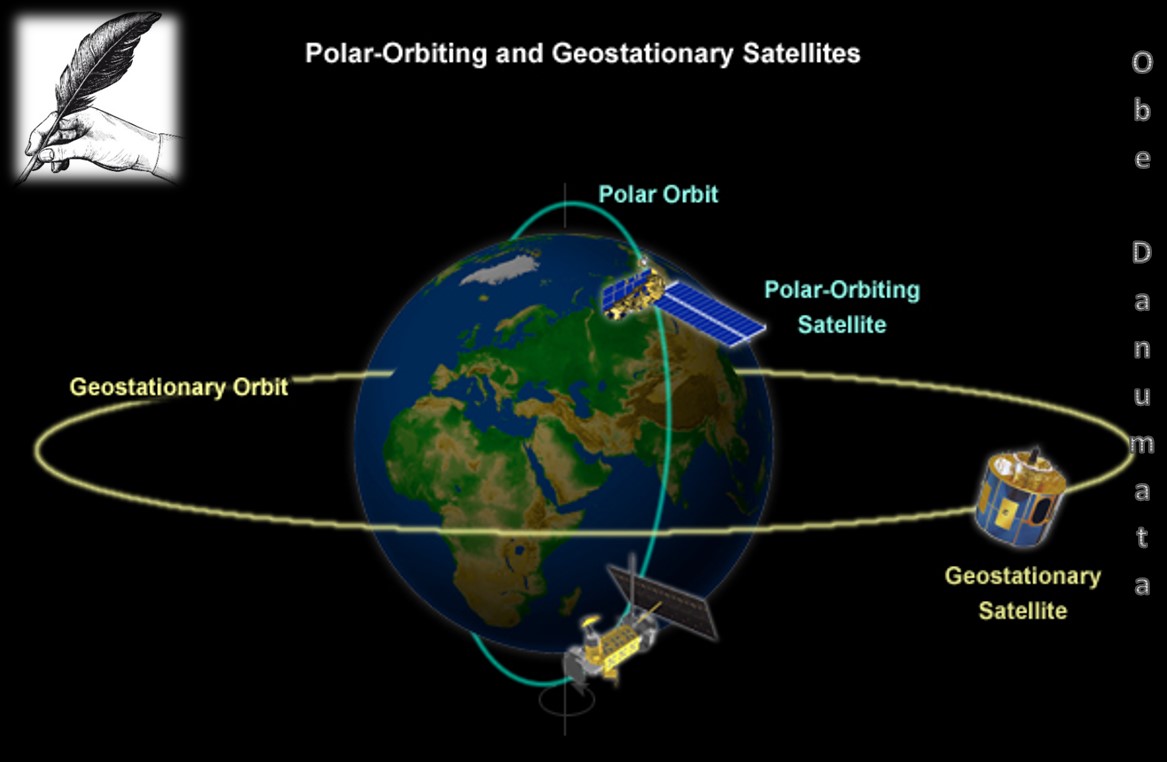
Another disadvantage of geostationary satellites is the incomplete geographical coverage, since ground stations at higher than roughly 60 degrees latitude have difficulty reliably receiving signals at low elevations. Satellite dishes in the Northern Hemisphere would need to be pointed almost directly towards the horizon. The signals would have to pass through the largest amount of atmosphere, and could even be blocked by land topography, vegetation or buildings. In the USSR, a practical solution was developed for this problem with the creation of special Molniya / Orbita inclined path satellite networks with elliptical orbits. Similar elliptical orbits are used for the Sirius Radio satellites.
Geostationary satellites have two major limitations. First, because the orbital zone is an extremely narrow ring in the plane of the equator, the number of satellites that can be maintained in geostationary orbits without mutual conflict (or even collision) is limited. Second, the distance that an electromagnetic (EM) signal must travel to and from a geostationary satellite is a minimum of 71,600 kilometers or 44,600 miles. Thus, a latency of at least 240 milliseconds is introduced when an EM signal, traveling at 300,000 kilometers per second (186,000 miles per second), makes a round trip from the surface to the satellite and back.
There are two other, less serious, problems with geostationary satellites. First, the exact position of a geostationary satellite, relative to the surface, varies slightly over the course of each 24-hour period because of gravitational interaction among the satellite, the earth, the sun, the moon, and the non-terrestrial planets. As observed from the surface, the satellite wanders within a rectangular region in the sky called the box. The box is small, but it limits the sharpness of the directional pattern, and therefore the power gain, that earth-based antennas can be designed to have. Second, there is a dramatic increase in background EM noise when the satellite comes near the sun as observed from a receiving station on the surface, because the sun is a powerful source of EM energy. This effect, known as solar fade, is a problem only within a few days of the equinoxes in late March and late September. Even then, episodes last for only a few minutes and take place only once a day.

Geostationary Orbit Speed
Satellite Orbits Includes:
Satellite orbit types & definitionsLow earth orbit, LEOGeostationary orbit, GEOHighly elliptical orbit HEOTechniques for launching satellites into orbit
One very popular orbit format is the geostationary satellite orbit. The geostationary orbit is used by many applications including direct broadcast as well as communications or relay systems.
The geostationary orbit has the advantage that the satellite remains in the same position throughout the day, and antennas can be directed towards the satellite and remain on track.
This factor is of particular importance for applications such as direct broadcast TV where changing directions for the antenna would not be practicable.
It is necessary to take care over the use of the abbreviations for geostationary orbit. Both GEO and GSO are seen, and both also used for geosynchronous orbit.
Geostationary orbit development
The idea of a geostationary orbit has been postulated for many years. One of the possible originators of the basic idea was a Russian theorist and science fiction writer, Konstantin Tsiolkovsky. However it was Herman Oberth and Herman Potocnik who wrote about orbiting stations at an altitude of 35 900 km above the Earth that had a rotational period of 24 hours making it appear to hover over a fixed point on the equator.
The next major step forwards occurred when Arthur C Clarke, the science fiction write, published a serious article in Wireless World, a major UK electronics and radio publication, in October 1945. The article was entitled 'Extra-Terrestrial Relays: Can Rocket Stations Give World Coverage?'
Clarke extrapolated what could be done with the German rocket technology of the day and looked at what might be possible in the future. He postulated that it would be possible to provide complete global coverage with just three geostationary satellites.
In the article, Clarke determined the orbital characteristics required as well as the transmitter power levels, the generation of solar power could be used, even calculating the impact of solar eclipses.
Clarke's article was well ahead of its time. It took until 1963 before NASA was able to start launching satellites that could test the theory. The first serviceable satellite able to start testing the theory was Syncom 2 which was launched on 26 July 1963. [Syncom 1 failed as it was unable to reach its correct geostationary orbit].
Geostationary orbit basics
As the height of a satellite increases, so the time for the satellite to orbit increases. At a height of 35790 km, it takes 24 hours for the satellite to orbit. This type of orbit is known as a geosynchronous orbit, i.e. it is synchronized with the Earth.
One particular form of geosynchronous orbit is known as a geostationary orbit. In this type of orbit the satellite rotates in the same direction as the rotation of the Earth and has an approximate 24 hour period. This means that it revolves at the same angular velocity as the Earth and in the same direction and therefore remains in the same position relative to the Earth.
In order to ensure that the satellite rotates at exactly the same speed as the Earth, it is necessary to clarify exactly what the time is for the rotation of the Earth. For most timekeeping applications, the Earth's rotation is measured relative to the Sun's mean position, and the rotation of the earth combined with the rotation around the Sun provide the length of time for a day. However this is not the exact rotation that we are interested in to give a geostationary orbit - the time required is just that for one rotation. This time period is known as a sidereal day and it is 23 hours 56 minutes and 4 seconds long.
Geometry dictates that the only way in which an orbit that rotates once per day can remain over exactly the same spot on the Earth's surface is that it moves in the same direction as the earth's rotation. Also it must not move north or south for any of its orbit. This can only occur if it remains over the equator.
Different orbits can be seen from the diagram. Emporia gazette garage sales. As all orbital planes need to pass through the geo-centre of the Earth, the two options available are shown. Even if both orbits rotate at the same speed as the Earth, the one labelled geosynchronous will move north of the equator for part of the day, and below for the other half - it will not be stationary. For a satellite to be stationary, it must be above the Equator.
Geostationary satellite drift
Even when satellites are placed into a geostationary orbit, there are several forces that can act on it to change its position slowly over time.
Factors including the earth's elliptical shape, the pull of the Sun and Moon and others act to increase the satellite orbital inclination. In particular the non-circular shape of the of the Earth around the Equator tends to draw the satellites towards two stable equilibrium points, one above the Indian Ocean and the other very roughly around the other side of the World. This results in what is termed as an east-west libration or movement back and forth.
To overcome these movements, fuel is carried by the satellites to enable them to carry out 'station-keeping' where the satellite is returned to its desired position. The period between station-keeping manoeuvres is determined by the allowable tolerance on the satellite which is mainly determined by the ground antenna beamwidth. This will mean that no re-adjustment of the antennas is required.
Often the useful life of a satellite is determined by the time for which fuel will allow the station-keeping to be undertaken. Often this will be several years. After this the satellite can drift towards one of the two equilibrium points, and possibly re-enter the Earth's atmosphere. The preferred option is for the satellites to utilise some last fuel to lift them into a higher and increasing orbit to prevent them from interfering with other satellites.
Geostationary orbit coverage
A single geostationary satellite obviously cannot provide complete global coverage. However, a single geostationary satellite can see approximately 42% of the Earth's surface with coverage falling off towards the satellite is not able to 'see' the surface. This occurs around the equator and also towards the polar regions.
For a constellation of three satellites equally spaced around the globe, it is possible to provide complete coverage around the equator and up to latitudes of 81° both north and south.

Other Iridium Phones:
A single geostationary satellite is on a line of sight with about 40 percent of the earth's surface. Three such satellites, each separated by 120 degrees of longitude, can provide coverage of the entire planet, with the exception of small circular regions centered at the north and south geographic poles. A geostationary satellite can be accessed using a directional antenna, usually a small dish, aimed at the spot in the sky where the satellite appears to hover. The principal advantage of this type of satellite is the fact that an earthbound directional antenna can be aimed and then left in position without further adjustment. Another advantage is the fact that because highly directional antennas can be used, interference from surface-based sources, and from other satellites, is minimized.
Derivation of geostationary altitude
In any circular orbit, the centripetal acceleration required to maintain the orbit is provided by the gravitational force on the satellite. To calculate the geostationary orbit altitude, one begins with this equivalence, and uses the fact that the orbital period is one sidereal day.
By Newton's second law of motion, we can replace the forces F with the mass m of the object multiplied by the acceleration felt by the object due to that force:
We note that the mass of the satellite m appears on both sides — geostationary orbit is independent of the mass of the satellite. So calculating the altitude simplifies into calculating the point where the magnitudes of the centripetal acceleration required for orbital motion and the gravitational acceleration provided by Earth's gravity are equal.
The centripetal acceleration's magnitude is:
where ? is the angular speed, and r is the orbital radius as measured from the Earth's center of mass.
The magnitude of the gravitational acceleration is:
where M is the mass of Earth, 5.9736 × 1024 kg, and G is the gravitational constant, 6.67428 ± 0.00067 × 10-11 m3 kg-1 s-2.
Equating the two accelerations gives:
The product GM is known with much greater accuracy than either factor; it is known as the geocentric gravitational constant µ = 398,600.4418 ± 0.0008 km3 s-2:
The angular speed ? is found by dividing the angle travelled in one revolution (360° = 2p rad) by the orbital period (the time it takes to make one full revolution: one sidereal day, or 86,164.09054 seconds).[3] This gives:
The resulting orbital radius is 42,164 kilometres (26,199 mi). Subtracting the Earth's equatorial radius, 6,378 kilometres (3,963 mi), gives the altitude of 35,786 kilometres (22,236 mi). Orbital speed (how fast the satellite is moving through space) is calculated by multiplying the angular speed by the orbital radius:
Orbite alocation
Satellites in geostationary orbit must all occupy a single ring above the equator. The requirement to space these satellites apart means that there are a limited number of orbital 'slots' available, thus only a limited number of satellites can be placed in geostationary orbit. This has led to conflict between different countries wishing access to the same orbital slots (countries at the same longitude but differing latitudes). These disputes are addressed through the International Telecommunication Union's allocation mechanism.[5] Countries located at the Earth's equator have also asserted their legal claim to control the use of space above their territory.[6] Since the Clarke Orbit is about 265,000 km (165,000 mi) long, countries and territories in less-populated parts of the world have been allocated slots already, even though they aren't used, yet. The problem presently lies over densely-populated areas such as the Americas and Europe/Africa, and above the middles of the three equatorial oceans.
Orbit Inclination
If a geosynchronous satellite's orbit is not exactly aligned with the equator, the orbit is known as an inclined orbit. It will appear (when viewed by someone on the ground) to oscillate daily around a fixed point in the sky. As the angle between the orbit and the equator decreases, the magnitude of this oscillation becomes smaller; when the orbit lies entirely over the equator, the satellite remains stationary relative to the Earth's surface – it is said to be geostationary.
Impact on signals
Satellites in geostationary orbits are far enough away from Earth that communication latency becomes very high — about a quarter of a second for a one-way trip from a ground based transmitter to a geostationary satellite and back, and close to half a second for round-trip end-to-end communication.
For example, for ground stations at latitudes of f=±45° on the same meridian as the satellite, the one-way delay can be computed by using the cosine rule, given the above derived geostationary orbital radius r, the Earth's radius R and the speed of light c, as
This presents problems for latency-sensitive applications such as voice communication or online gaming.
Application
There are approximately 300 operational geosynchronous satellites. Geostationary satellites appear to be fixed over one spot above the equator. Receiving and transmitting antennas on the earth do not need to track such a satellite. These antennas can be fixed in place and are much less expensive than tracking antennas. These satellites have revolutionized global communications, television broadcasting and weather forecasting, and have a number of important defense and intelligence applications.
One disadvantage of geostationary satellites is a result of their high altitude: radio signals take approximately 0.25 of a second to reach and return from the satellite, resulting in a small but significant signal delay. This delay increases the difficulty of telephone conversation and reduces the performance of common network protocols such as TCP/IP, but does not present a problem with non-interactive systems such as television broadcasts. There are a number of proprietary satellite data protocols that are designed to proxy TCP/IP connections over long-delay satellite links -- these are marketed as being a partial solution to the poor performance of native TCP over satellite links. TCP presumes that all loss is due to congestion, not errors, and probes link capacity with its 'slow-start' algorithm, which only sends packets once it is known that earlier packets have been received. Slow start is very slow over a path using a geostationary satellite.
Another disadvantage of geostationary satellites is the incomplete geographical coverage, since ground stations at higher than roughly 60 degrees latitude have difficulty reliably receiving signals at low elevations. Satellite dishes in the Northern Hemisphere would need to be pointed almost directly towards the horizon. The signals would have to pass through the largest amount of atmosphere, and could even be blocked by land topography, vegetation or buildings. In the USSR, a practical solution was developed for this problem with the creation of special Molniya / Orbita inclined path satellite networks with elliptical orbits. Similar elliptical orbits are used for the Sirius Radio satellites.
Geostationary satellites have two major limitations. First, because the orbital zone is an extremely narrow ring in the plane of the equator, the number of satellites that can be maintained in geostationary orbits without mutual conflict (or even collision) is limited. Second, the distance that an electromagnetic (EM) signal must travel to and from a geostationary satellite is a minimum of 71,600 kilometers or 44,600 miles. Thus, a latency of at least 240 milliseconds is introduced when an EM signal, traveling at 300,000 kilometers per second (186,000 miles per second), makes a round trip from the surface to the satellite and back.
There are two other, less serious, problems with geostationary satellites. First, the exact position of a geostationary satellite, relative to the surface, varies slightly over the course of each 24-hour period because of gravitational interaction among the satellite, the earth, the sun, the moon, and the non-terrestrial planets. As observed from the surface, the satellite wanders within a rectangular region in the sky called the box. The box is small, but it limits the sharpness of the directional pattern, and therefore the power gain, that earth-based antennas can be designed to have. Second, there is a dramatic increase in background EM noise when the satellite comes near the sun as observed from a receiving station on the surface, because the sun is a powerful source of EM energy. This effect, known as solar fade, is a problem only within a few days of the equinoxes in late March and late September. Even then, episodes last for only a few minutes and take place only once a day.
Geostationary Orbit Speed
Satellite Orbits Includes:
Satellite orbit types & definitionsLow earth orbit, LEOGeostationary orbit, GEOHighly elliptical orbit HEOTechniques for launching satellites into orbit
One very popular orbit format is the geostationary satellite orbit. The geostationary orbit is used by many applications including direct broadcast as well as communications or relay systems.
The geostationary orbit has the advantage that the satellite remains in the same position throughout the day, and antennas can be directed towards the satellite and remain on track.
This factor is of particular importance for applications such as direct broadcast TV where changing directions for the antenna would not be practicable.
It is necessary to take care over the use of the abbreviations for geostationary orbit. Both GEO and GSO are seen, and both also used for geosynchronous orbit.
Geostationary orbit development
The idea of a geostationary orbit has been postulated for many years. One of the possible originators of the basic idea was a Russian theorist and science fiction writer, Konstantin Tsiolkovsky. However it was Herman Oberth and Herman Potocnik who wrote about orbiting stations at an altitude of 35 900 km above the Earth that had a rotational period of 24 hours making it appear to hover over a fixed point on the equator.
The next major step forwards occurred when Arthur C Clarke, the science fiction write, published a serious article in Wireless World, a major UK electronics and radio publication, in October 1945. The article was entitled 'Extra-Terrestrial Relays: Can Rocket Stations Give World Coverage?'
Clarke extrapolated what could be done with the German rocket technology of the day and looked at what might be possible in the future. He postulated that it would be possible to provide complete global coverage with just three geostationary satellites.
In the article, Clarke determined the orbital characteristics required as well as the transmitter power levels, the generation of solar power could be used, even calculating the impact of solar eclipses.
Clarke's article was well ahead of its time. It took until 1963 before NASA was able to start launching satellites that could test the theory. The first serviceable satellite able to start testing the theory was Syncom 2 which was launched on 26 July 1963. [Syncom 1 failed as it was unable to reach its correct geostationary orbit].
Geostationary orbit basics
As the height of a satellite increases, so the time for the satellite to orbit increases. At a height of 35790 km, it takes 24 hours for the satellite to orbit. This type of orbit is known as a geosynchronous orbit, i.e. it is synchronized with the Earth.
One particular form of geosynchronous orbit is known as a geostationary orbit. In this type of orbit the satellite rotates in the same direction as the rotation of the Earth and has an approximate 24 hour period. This means that it revolves at the same angular velocity as the Earth and in the same direction and therefore remains in the same position relative to the Earth.
In order to ensure that the satellite rotates at exactly the same speed as the Earth, it is necessary to clarify exactly what the time is for the rotation of the Earth. For most timekeeping applications, the Earth's rotation is measured relative to the Sun's mean position, and the rotation of the earth combined with the rotation around the Sun provide the length of time for a day. However this is not the exact rotation that we are interested in to give a geostationary orbit - the time required is just that for one rotation. This time period is known as a sidereal day and it is 23 hours 56 minutes and 4 seconds long.
Geometry dictates that the only way in which an orbit that rotates once per day can remain over exactly the same spot on the Earth's surface is that it moves in the same direction as the earth's rotation. Also it must not move north or south for any of its orbit. This can only occur if it remains over the equator.
Different orbits can be seen from the diagram. Emporia gazette garage sales. As all orbital planes need to pass through the geo-centre of the Earth, the two options available are shown. Even if both orbits rotate at the same speed as the Earth, the one labelled geosynchronous will move north of the equator for part of the day, and below for the other half - it will not be stationary. For a satellite to be stationary, it must be above the Equator.
Geostationary satellite drift
Even when satellites are placed into a geostationary orbit, there are several forces that can act on it to change its position slowly over time.
Factors including the earth's elliptical shape, the pull of the Sun and Moon and others act to increase the satellite orbital inclination. In particular the non-circular shape of the of the Earth around the Equator tends to draw the satellites towards two stable equilibrium points, one above the Indian Ocean and the other very roughly around the other side of the World. This results in what is termed as an east-west libration or movement back and forth.
To overcome these movements, fuel is carried by the satellites to enable them to carry out 'station-keeping' where the satellite is returned to its desired position. The period between station-keeping manoeuvres is determined by the allowable tolerance on the satellite which is mainly determined by the ground antenna beamwidth. This will mean that no re-adjustment of the antennas is required.
Often the useful life of a satellite is determined by the time for which fuel will allow the station-keeping to be undertaken. Often this will be several years. After this the satellite can drift towards one of the two equilibrium points, and possibly re-enter the Earth's atmosphere. The preferred option is for the satellites to utilise some last fuel to lift them into a higher and increasing orbit to prevent them from interfering with other satellites.
Geostationary orbit coverage
A single geostationary satellite obviously cannot provide complete global coverage. However, a single geostationary satellite can see approximately 42% of the Earth's surface with coverage falling off towards the satellite is not able to 'see' the surface. This occurs around the equator and also towards the polar regions.
For a constellation of three satellites equally spaced around the globe, it is possible to provide complete coverage around the equator and up to latitudes of 81° both north and south.
The lack of polar coverage is not a problem for most users, although where polar coverage is needed, satellites using other forms of orbit are needed.
Geostationary orbit and path length / delay
One of the issues with using satellites in a geostationary orbit is the delay introduced by the path length.
The path length to any geostationary satellite is a minimum of 22300 miles. This assumes that the user is directly underneath the satellite to provide the shortest path length. In reality the user is unlikely to be in this position and the path length will be longer.
Assuming the shortest path length, this gives a single trip i.e. to the satellite or back of a minimum of around 120 milli-seconds. This means that the round trip from the ground to the satellite and back is roughly a quarter of a second.
Therefore to obtain a response in a conversation can take half a second as the signal must pass through the satellite twice - once on the outward journey to the remote listener, and then again with the response. This delay can make telephone conversations rather difficult when satellite links are used. It can also be seen when news reporters as using satellite links. When asked a question from the broadcasters studio, the reporter appears to take some time to answer. This delay is the reason why many long distance links use cables rather than satellites as the delays incurred are far less.
Advantages and disadvantages of geostationary orbit satellites
While the geostationary orbit is widely used for many satellite applications it is not suitable for all situations. There are several advantages and disadvantages to be taken into consideration:
Geostationary orbit advantages:
- Satellite always in same position relative to earth - antennas do not need re-orientation
Geostationary orbit disadvantages:
- Long path length, and hence losses when compared to LEO, or MEO.
- Satellites more costly to install in GEO in view of greater altitude.
- Long path length introduces delays.
- Geostationary satellite orbits can only be above the equator and therefore polar regions cannot be covered.
Despite the disadvantages of using satellites in geostationary orbit, they are still widely used because of the overriding advantage of the satellite always being in the same position relative to a given place on the Earth.
Geostationary Orbit Radius
More Essential Satellite Topics:
Interesting facts about satellites Satellite orbits Solar outage
Return to Satellite topics menu . . .
